Dicey Odds
In Dungeon Fodder, there are numerous actions which are guided by chance. Success rates for combat, success rates for opening a trapped treasure chest, success rates for everything! Being a fan of pen & paper tabletop gaming, I’m biased towards the dice as a means of simulating random events.
Even after coming to the conclusion that using dice would be the most accessible method of determining random events in the game, the number of die was another issue that had to be looked into. A colleague brought into my attention that the odds are radically different when using different numbers of dice.
For example, a single die roll is pretty simple to think about and calculate your probabilities. On a regular 6 sided die, you have a 1/6 chance of getting a certain number. Thats about a 17% chance which ain’t bad.
Using two dice however ups the odds somewhat.

This is a simple table of all probably outcomes of rolling two dice simultaneously. There are 36 different combinations possible but that does not mean your odds of getting a certain combination is 1/36 (about 3%).
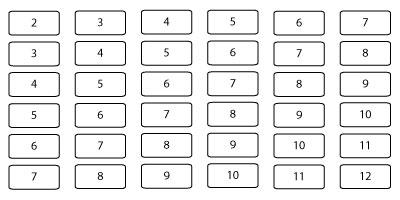
Here is the same table but now, it is based on total outcome of both dice.
Now, to count the odds.
- You have 1/36 (2.8%) chance of getting a 2 or a 12
- 1/18 (5.6%) chance of getting a 3 or an 11
- 1/12 (8.3%) chance of getting a 4 or a 10
- 1/9 (11%) chance of a 5 or a 9
- 5/36 (13.8%) chance of a 6 or an 8
- 1/6 (17%) chance of a 7
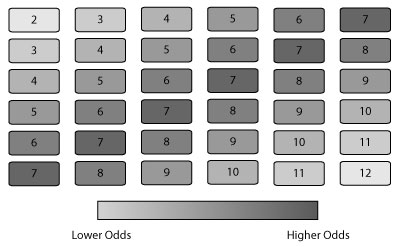
Not that this is really important but its interesting to know. If rolling items from a specific table, common items should definately be placed on the Higher Odds portion of the table, (probably a 7) while overpowering items are placed on the lowest odds portion (maybe on a roll of a 2 or 12).
Majority of the results in Dungeon Fodder relies on a the results of a single die. I find this to be more straightforward and improves upon the pacing of the game. Some feedback has stated that there might be too many die rolls therefore that has to be looked into as well.

